通过拟合计算提高FFT幅度谱求频率的分辨率

1. 问题描述 ​

当信号为单一频率成分，但其频率不在FFT分辨率点上时，无法直接通过FFT幅度谱峰值点获得精确频率。

在单一信号频率无噪声的情况下，幅度谱的‘形状’只和频率有关，和信号的幅度与相位无关（这里的形状可以指归一化幅度谱）。因此可以尝试通过幅度谱的形状推导出频率。

本文通过数学推导得出幅度谱比值和频率的关系，从而得到频率插值的公式。

def fit_func1(x0, x1, x2, y0, y1, y2):
    assert y1 >= y0 and y1 >= y2
    a = x1
    b = -1 if (y0 > y2) else 1
    r = y1 / (y0 if (y0 > y2) else y2)
    x_peak = a + b / (r + 1)
    return x_peak

具体的Python实验：非整数倍周期信号FFT影响.py

该方法的实际应用：idx_estimation()函数：通过中心点的幅度谱值与相邻点的幅度谱值，估计出更精确的坐标

2. 数学模型 ​

2.1 信号定义 ​

考虑归一化频率为 $f$ 的复指数信号：

$$x[n] = e^{j2\pi f n}, \quad n=0,1,\cdots,N-1$$

其DFT定义为：

$$X[k] = \sum_{n=0}^{N-1} x[n] e^{-j2\pi kn/N}$$

2.2 等比数列求和 ​

将信号表达式代入DFT：

$$X[k] = \sum_{n=0}^{N-1} e^{j2\pi f n} \cdot e^{-j2\pi kn/N} = \sum_{n=0}^{N-1} e^{j2\pi n (f - k/N)}$$

这是一个首项为 $a_1 = 1$，公比为 $r = e^{j2\pi (f - k/N)}$ 的等比数列。等比数列求和公式为：

$$S_N = a_1 \frac{1 - r^N}{1 - r}$$

代入参数：

$$X[k] = \frac{1 - [e^{j2\pi (f - k/N)}]^N}{1 - e^{j2\pi (f - k/N)}}$$

2.3 简化表达式 ​

化简分子：

$$[e^{j2\pi (f - k/N)}]^N = e^{j2\pi N(f - k/N)} = e^{j2\pi (Nf - k)}$$

由于 $k$ 是整数，$e^{-j2\pi k} = 1$，所以：

$$e^{j2\pi (Nf - k)} = e^{j2\pi Nf}$$

因此分子简化为：

$$1 - e^{j2\pi Nf}$$

最终DFT表达式为：

$$X[k] = \frac{1 - e^{j2\pi Nf}}{1 - e^{j2\pi (f - k/N)}}$$

2.4 幅度谱表达式 ​

幅度谱为：

$$|X[k]| = \left| \frac{1 - e^{j2\pi Nf}}{1 - e^{j2\pi (f - k/N)}} \right|$$

利用复指数性质 $|1 - e^{j\theta}| = 2|\sin(\theta/2)|$：

$$|X[k]| = \frac{|\sin(\pi Nf)|}{|\sin[\pi (f - k/N)]|}$$

3. 任意两点幅度比值计算 ​

3.1 分类讨论 ​

$|X[k]|$表达式的分子是一个不随序号$k$改变的值，那么通过相除可以去掉该项

考虑频点 $a$ 和 $b$，其幅度比为：

$$\frac{|X[a]|}{|X[b]|} = \frac{|\sin[\pi (f - a/N)]|^{-1}}{|\sin[\pi (f - b/N)]|^{-1}} = \frac{|\sin[\pi (f - b/N)]|}{|\sin[\pi (f - a/N)]|}$$

当 $f-b/N$ 的值非常小时，可以应用近似：

$$sin(x) = x$$

因此我们取点峰值点$k_1$与相邻点$k_1 \pm 1$计算比值

在峰值邻域（$k_1$及其相邻点），设$f = \frac{k_1 + \delta}{N}$，则：

1. 峰值点$k_1$：

$$|X[k_1]| \propto \frac{1}{|\sin(\pi \delta/N)|}$$

2. 相邻点$k_1 \pm 1$：

$$|X[k_1 \pm 1]| \propto \frac{1}{|\sin[\pi (\delta \mp 1)/N]|}$$

情况1：$\delta \geq 0$(取右侧点$k_1+1$)

$$r = \frac{|X[k_1]|}{|X[k_1+1]|} = \frac{|\sin[\pi (\delta - 1)/N]|}{|\sin(\pi \delta/N)|}$$

当$N$较大时，小角度近似$\sin\theta \approx \theta$：

$$r \approx \frac{|\pi (\delta - 1)/N|}{|\pi \delta/N|} = \frac{|1 - \delta|}{\delta} = \frac{1 - \delta}{\delta}$$

解得：

$$\delta \approx \frac{1}{r + 1}$$

情况2：$\delta < 0$(取左侧点$k_1-1$)

$$r = \frac{|X[k_1]|}{|X[k_1-1]|} = \frac{|\sin[\pi (\delta + 1)/N]|}{|\sin(\pi \delta/N)|} \approx \frac{|1 + \delta|}{|\delta|} = -\frac{1 + \delta}{\delta}$$

解得：

$$\delta \approx \frac{-1}{r + 1}$$

3.2 统一表达式 ​

两种情况的解可统一表示为：

$$\delta \approx \frac{b}{r + 1}$$

其中：

$$b = \begin{cases} 1 & \delta \geq 0 \\ -1 & \delta < 0 \end{cases}$$

综上 ​

我们计算拟合频点的方法为

1. 找到幅度谱$|X|$ 的峰值点 $k_1$ 以及相邻点中较大的点 $k_1 \pm 1$
2. 计算 $r = \frac{|X[k_1]|}{|X[k_1 \pm 1]|}$， b = $1$ or $-1$
3. 根据 $r$ DFT频点 $fN$

   $$fN = k_1 + \delta = k_1 + \frac{b}{r + 1} , b = \begin{cases} 1 & \delta \geq 0 \\ -1 & \delta < 0 \end{cases}$$

4. 其他 ​

假如选择峰值点和较小的相邻点推导，公式为

$$fN = k_1 + \frac{b}{1-r} , b = \begin{cases} 1 & \delta \geq 0 \\ -1 & \delta < 0 \end{cases}$$

5. 实验 ​

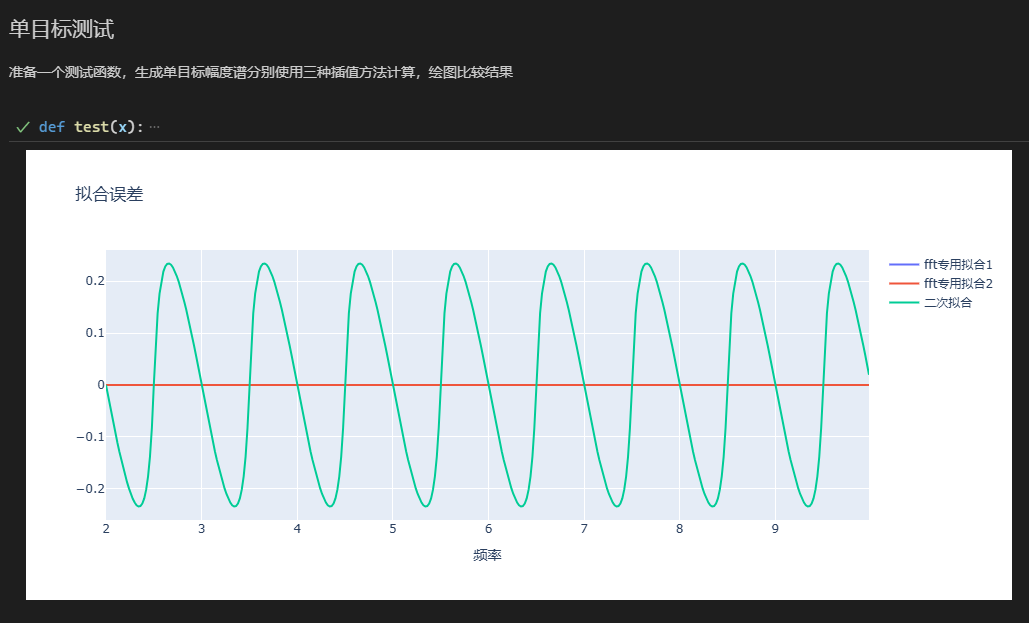
此处展示非整数倍周期信号FFT影响.py的运行结果

1. 测试不同频率的正弦信号下通过幅度谱峰值计算频率的误差

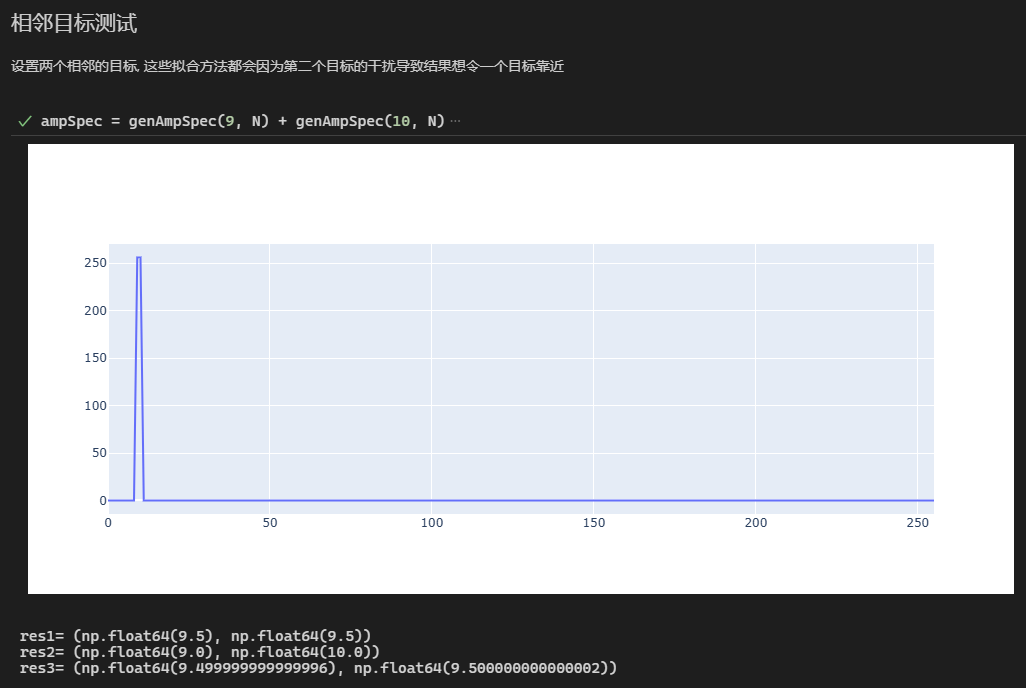
2. 生成一个包含两种频率成分的信号，搜索幅度谱峰值后进行插值求频率