Capon算法（MVDR 波束形成器）原理与简单仿真

2.1k
信号处理算法

Capon算法，也称为最小方差无失真响应（Minimum Variance Distortionless Response, MVDR）波束形成器。Capon算法的主要目标是通过调整阵列天线的加权系数，使得在期望信号方向上保持无失真响应，同时最小化来自其他方向的干扰和噪声能量。

Capon算法原理 ​

信号模型 ​

在线性调频毫米波雷达的信号处理中，我们常常会先对接收到的信号根据距离维度或者速度维度分离，再测角。傅里叶变化并再频域分离后的信号，是非常标准的窄带信号（FFT本身可以视为窄带滤波器组）。因此在建立信号模型时，我们将信号假设为一个窄带信号。

信号带宽较窄的情况下，信号的频率成分集中，相邻频率分量的相位变化相对缓慢，从而在空间阵列上的时间延迟可以直接通过相位差来体现。再次基础上我们可以用相位差大大简化信号模型。

设现在存在 MM 个阵元 pp 个信号源，一帧数据供 NN 个快拍。

x(n)=As(n)+n(n)\begin{equation} \boldsymbol{x}(n)=\boldsymbol{A} \boldsymbol{s}(n)+ \boldsymbol{n}(n) \end{equation}

  • x(n)\boldsymbol{x}(n)： 表示系统的输入信号， x(n)\boldsymbol{x}(n) 是一个 M×1M\times 1 的列向量，分别表示 MM 个阵元接收到的信号。

  • s(n)\boldsymbol{s}(n)： 并表示信号源发送过来的信号。一般选择其中1个阵元作为参考阵元，s(n)=[s1(n)s2(n)⋮sp(n)]\boldsymbol{s}(n) = \begin{bmatrix} s_{1}(n) \\ s_{2}(n) \\ \vdots \\ s_{p}(n) \end{bmatrix} , si(n)s_{i}(n) 表示参考阵元接收到的第 ii 信号源的信号。

  • A\boldsymbol{A}: 是一个 M×pM\times p 的到达矢量矩阵，每一列都是一个到达矢量(arrival vector)，A=[a(ω1),a(ω2),⋯ ,a(ωp)]\boldsymbol{A}=[\boldsymbol{a}(\omega_{1}),\boldsymbol{a}(\omega_{2}), \cdots ,\boldsymbol{a}(\omega_{p})]，用于表示不同阵元接收到的信号的差异，通常 x1(n)x_{1}(n) 是参考阵元的接受信号， 此时 AA 的第一行为 [1,1,⋯ ,1][1,1,\cdots,1] 。

  • n(n)\boldsymbol{n}(n): 表示噪声，是M×1M\times 1 的列向量。

设计权向量 w\boldsymbol{w} ​

系统接收到的信号 x(n)\boldsymbol{x}(n) 中叠加了多个信号源的信号。我们希望设计一个权向量 w\boldsymbol{w} 使得波束形成器的输出能够抽取出想要的信号源的方向，同时使得输出信号的总功率尽量的小。

我们先将这个系统简单描述成一下公式：

y(n)=wHx(n)\begin{equation} y(n) = \boldsymbol{w}^{H}\boldsymbol{x}(n) \end{equation}

假设我们的目标时要从 pp 个信号源的信号 s(n)\boldsymbol{s}(n) 中把我们想要的信号源 kk 的信号 sk(n)s_{k}(n) 分离出来。

首先将 x(n)\boldsymbol{x}(n) 拆分：

x(n)=a(ωk)sk(n)+∑i=1,i≠kpa(ωi)si(n)+n(n)\begin{equation} \boldsymbol{x}(n) = \boldsymbol{a}(\omega_{k}) s_{k}(n) +\displaystyle\sum_{i=1,i \neq k}^{p} \boldsymbol{a}(\omega_{i}) s_{i}(n) + \boldsymbol{n}(n) \end{equation}

式子中的三项分别表示：期望得到的信号、其他干扰信号、噪声。将 (3)(3) 代入 (2)(2) 得：

y(n)=wH[a(ωk)sk(n)+∑i=1,i≠kpa(ωi)si(n)+n(n)]y(n)=wHa(ωk)sk(n)+∑i=1,i≠kpwHa(ωi)si(n)+wHn(n)\begin{align} y(n) &= \boldsymbol{w}^{H}[ \boldsymbol{a}(\omega_{k}) s_{k}(n) + \displaystyle\sum_{i=1,i \neq k}^{p} \boldsymbol{a}(\omega_{i}) s_{i}(n) + \boldsymbol{n}(n) ] \\ y(n) &= \boldsymbol{w}^{H} \boldsymbol{a}(\omega_{k}) s_{k}(n) + \displaystyle\sum_{i=1,i \neq k}^{p} \boldsymbol{w}^{H} \boldsymbol{a}(\omega_{i}) s_{i}(n) + \boldsymbol{w}^{H} \boldsymbol{n}(n) \end{align}

假如我们希望保留期望信号 sk(n)s_{k}(n) 同时减少其他干扰信号 si(n),i≠ks_{i}(n) ,i \neq k 的功率，则权向量需要满足一下公式：

wHa(ωk)=1（波束形成条件）wHa(ωi)=0,ωi≠ωk（零点形成条件）\begin{alignat}{2} \boldsymbol{w}^{H} \boldsymbol{a}(\omega_{k}) &= 1 &\text{（波束形成条件）} \\ \boldsymbol{w}^{H} \boldsymbol{a}(\omega_{i}) &= 0 , \omega_{i} \neq \omega_{k} &\text{（零点形成条件）} \end{alignat}

由于信号源方向 ωi\omega_{i} 是未知的，仅仅依靠以上两个条件难以推导权向量 w\boldsymbol{w}。因此我们使用另一个思路：在满足式 (6):wHa(ωk)=1(6): \boldsymbol{w}^{H} \boldsymbol{a}(\omega_{k}) = 1 的前提下，令系统输出 y(n)y(n) 的功率尽量的小。

y(n)y(n) 的功率可以表示为：

E{∣y(n)∣2}=lim⁡N→∞∑n=1N∣y(n)∣2=wHRxxw\begin{equation} E\{|y(n)|^{2}\} = \lim_{N \to \infty} \displaystyle\sum_{n=1}^{N} |y(n)|^{2} = \boldsymbol{w}^{H} \boldsymbol{R_{xx}} \boldsymbol{w} \end{equation}

我们现在求解的问题是: 在约束条件 (6)(6) 的情况下，求得令 E{∣y(n)∣2}E\{|y(n)|^{2}\} 最小的权向量 w\boldsymbol{w} ，用公式表达如下：

约束条件 wHa(ωk)=1\boldsymbol{w}^{H} \boldsymbol{a}(\omega_{k}) = 1 代表无失真，期望令 E{∣y(n)∣2}E\{|y(n)|^{2}\} 最小对应最小方差，合起来就是‘最小方差无失真’,所以常常将Capon算法称为‘最小方差无失真响应波束形成器(MVDR beamformer)’

min⁡wE{∣y(n)∣2}=wHRxxwsubject towHa(ωk)=1\begin{equation} \begin{aligned} & \min_{\boldsymbol{w}} \quad E\{|y(n)|^{2}\} = \boldsymbol{w}^{H} \boldsymbol{R_{xx}} \boldsymbol{w} \\ & \text{subject to} \quad \boldsymbol{w}^{H} \boldsymbol{a}(\omega_{k}) = 1 \end{aligned} \end{equation}

使用拉格朗日乘数法(Lagrange multiplier)求解这一优化问题。首先构造目标函数：

J(w)=wHRxxw+λ[1−wHa(ωk)]\begin{equation} J(\boldsymbol{w}) = \boldsymbol{w}^{H} \boldsymbol{R_{xx}} \boldsymbol{w} + \lambda [1 - \boldsymbol{w}^{H} \boldsymbol{a}(\omega_{k})] \end{equation}

其中 λ\lambda 为拉格朗日乘数。令 J(w)J(\boldsymbol{w}) 的导数为0：

∂J(w)∂w=0Rxxw−λa(ωk)=0\begin{align} \frac{\partial J(\boldsymbol{w})}{\partial \boldsymbol{w}} = 0 \\ \boldsymbol{R_{xx}} \boldsymbol{w} - \lambda \boldsymbol{a}(\omega_{k}) &= 0 \end{align}

进一步计算如下：

λa(ωk)=RxxwλRxx−1a(ωk)=wλa(ωk)HRxx−1a(ωk)=a(ωk)Hw=1λ=1a(ωk)HRxx−1a(ωk)\begin{equation} \begin{aligned} \lambda \boldsymbol{a}(\omega_{k}) &= \boldsymbol{R_{xx}} \boldsymbol{w} \\ \lambda \boldsymbol{R_{xx}^{-1}} \boldsymbol{a}(\omega_{k}) &= \boldsymbol{w} \\ \lambda \boldsymbol{a}(\omega_{k})^{H} \boldsymbol{R_{xx}^{-1}} \boldsymbol{a}(\omega_{k}) &= \boldsymbol{a}(\omega_{k})^{H} \boldsymbol{w} =1 \\ \lambda &= \frac{1}{\boldsymbol{a}(\omega_{k})^{H} \boldsymbol{R_{xx}^{-1}} \boldsymbol{a}(\omega_{k})} \\ \end{aligned} \end{equation}

将 λ\lambda 重新代回去计算 wopt\boldsymbol{w}_{opt} ：

wopt=Rxx−1a(ωk)a(ωk)HRxx−1a(ωk)\begin{equation} \boldsymbol{w}_{opt} = \frac{\boldsymbol{R_{xx}^{-1}} \boldsymbol{a}(\omega_{k})}{\boldsymbol{a}(\omega_{k})^{H} \boldsymbol{R_{xx}^{-1}} \boldsymbol{a}(\omega_{k})} \end{equation}

将 wopt\boldsymbol{w}_{opt} 带入式 (8)(8) 可以得到 Capon空间谱:

PCapon(ω)=1a(ω)HRxx−1a(ω)\begin{equation} P_{Capon}(\omega) = \frac{1}{\boldsymbol{a}(\omega)^{H} \boldsymbol{R_{xx}^{-1}} \boldsymbol{a}(\omega)} \end{equation}

遍历所有 ω\omega 值， 得到 Capon空间谱并找到 pp 个峰值，每一个峰值对应的ω\omega 值即为波束方向。

matlab程序仿真 ​

matlab提供了两个Cpaon算法的函数phased.MVDREstimator 和 phased.MVDREstimator2D，分别是一维和二维的测角。

这边在matlab例子的基础上自己实现一遍Capon算法，对比一下结果是否一致

matlab的例子可以用下面的指令打开

matlab
openExample('phased/EstimateDOATwoSignalsUsingMVDRExample')

完整代码 ​

matlab
clear; clc; close all
%% 初始化参数，生成阵列信号

fs = 8000;
t = (0:1 / fs:1).';
x1 = cos(2 * pi * t * 300);
x2 = cos(2 * pi * t * 400);
% 生成均匀线阵
array = phased.ULA('NumElements', 10, 'ElementSpacing', 1);
array.Element.FrequencyRange = [100e6 300e6];
fc = 150.0e6;
x = collectPlaneWave(array, [x1 x2], [-10 0; 60 0]', fc);
noise = 0.1 * (randn(size(x)) + 1i * randn(size(x)));
signal = x + noise;
axis_angle = (-90:1:90);

%% Capon谱 phased.MVDREstimator
estimator = phased.MVDREstimator('SensorArray', array, 'ScanAngles', axis_angle, ...
    'OperatingFrequency', fc, 'DOAOutputPort', true, 'NumSignals', 2);
[y, doas] = estimator(signal);
doas = broadside2az(sort(doas), [20 -5])

%% Capon谱

addpath '.\function'
% 获取阵元坐标
ula_pos = getElementPosition(array);
% 计算到达矢量
steering_vectors = steering_vector(ula_pos, [axis_angle; zeros(size(axis_angle))], physconst('LightSpeed') / fc);
% 去直流 转置
x = transpose(signal - mean(signal, 1));
% 自协方差矩阵
Cxx = x * x';
my_mvdr_spec = 1 ./ sum(steering_vectors' / Cxx .* steering_vectors.', 2);
my_mvdr_spec = abs(my_mvdr_spec);
my_mvdr_spec = sqrt(my_mvdr_spec);

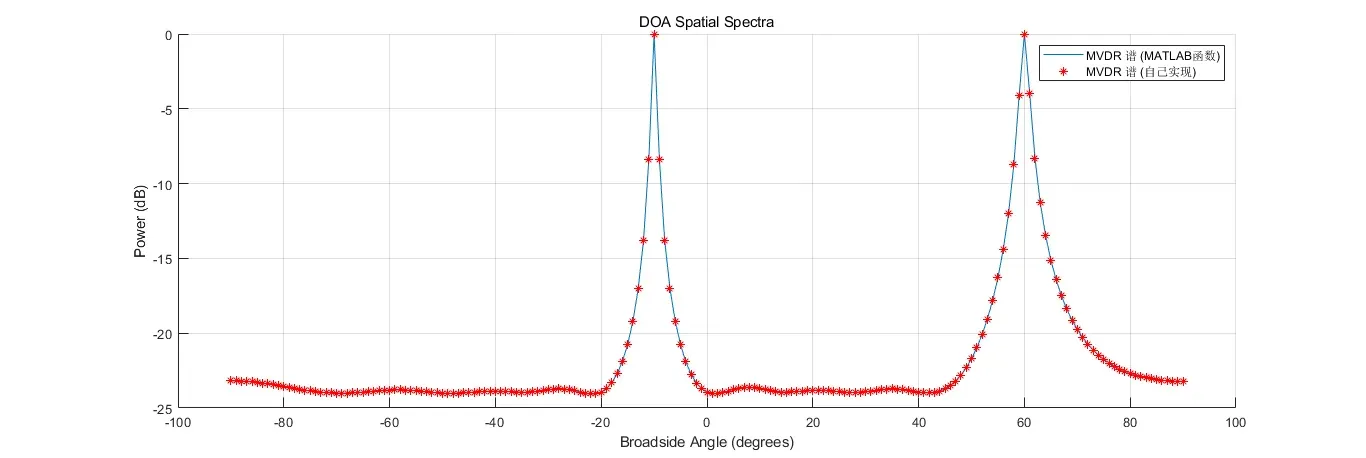
figure("Name", "Capon 算法测角")

hold on;
helperPlotSpec(axis_angle, y, 'MVDR 谱 (MATLAB函数)');
helperPlotSpec(axis_angle, my_mvdr_spec, 'MVDR 谱 (自己实现)', 'r*');
hold off;

详解 ​

第一步是计算遍历角度是用到的导向矢量,sv = steering_vector(pos, ang, lambda) 函数输入阵元位置、角度、信号波长，输出导向矢量,详细解释可以看 到达矢量 (Arrival vector)，源文件见steering_vector.m

matlab
% 获取阵元坐标
ula_pos = getElementPosition(array);
% 计算到达矢量
steering_vectors = steering_vector(ula_pos, [axis_angle; zeros(size(axis_angle))], physconst('LightSpeed') / fc);

然后计算协方差矩阵，matlab的例程得到的信号x是一个行向量矩阵，所以先转置，在计算协方差矩阵

matlab
% 去直流 转置
x = transpose(signal - mean(signal, 1));
% 自协方差矩阵
Cxx = x * x';

得到协方差矩阵和导向矢量后，就可以按照 PCapon(ω)=1a(ω)HRxx−1a(ω)P_{Capon}(\omega) = \frac{1}{\boldsymbol{a}(\omega)^{H} \boldsymbol{R_{xx}^{-1}} \boldsymbol{a}(\omega)} 计算空间谱了。

这里的steering_vectors中包含了多个导向矢量，可以用循环一个一个计算，也可以按照下面的方法算。最后还开根号了，这一步在实际应用中是没有必要的，只是为了和matlab的phased.MVDREstimator得到的结果一致。

matlab
my_mvdr_spec = 1 ./ sum(steering_vectors' / Cxx .* steering_vectors.', 2);
my_mvdr_spec = abs(my_mvdr_spec);
my_mvdr_spec = sqrt(my_mvdr_spec);

结果 ​

doas =

  -10.6490   60.3813
Capon 算法测角
到达矢量 (Arrival vector)
MUSIC算法